Statically indeterminate reaction force analysis

Problem description:

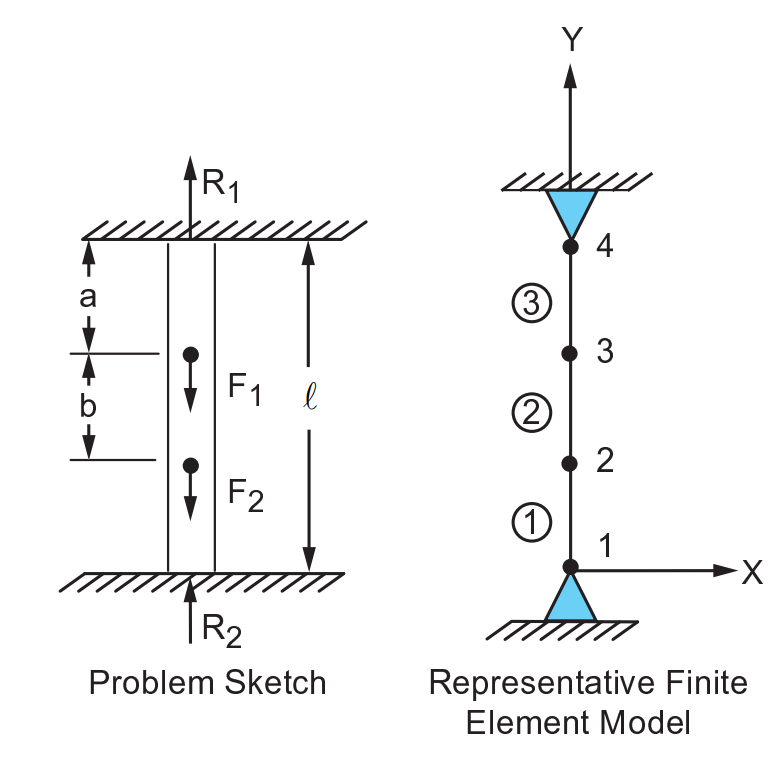
• A prismatical bar with built-in ends is loaded axially at two intermediate cross sections. Determine the reactions \(R_1\) and \(R_2\).

Reference:

• S. Timoshenko, Strength of Materials, Part I, Elementary Theory and Problems, 3rd Edition, D. Van Nostrand Co., Inc., New York, NY, 1955, pg. 26, problem 10.

Analysis type(s):

• Static Analysis ANTYPE=0

Element type(s):

• 3-D Spar (or Truss) Elements (LINK180)

Material properties

• \(E = 30 \cdot 10^6 psi\)

Geometric properties:

• \(a = b = 0.3\)

• \(l = 10 in\)

Loading:

• \(F_1 = 2*F_2 = 1000 lb\)

Analytical equations:

• \(P = R_1 + R_2\) where \(P\) is load.

• \(\frac{R_2}{R_1} = \frac{a}{b}\) Where \(a\) and \(b\) are the ratios of distances between the load and the wall.

# sphinx_gallery_thumbnail_path = '_static/vm1_setup.png'

from ansys.mapdl.core import launch_mapdl

# start mapdl and clear it
mapdl = launch_mapdl()
mapdl.clear()  # optional as MAPDL just started

# enter verification example mode and the pre-processing routine
mapdl.verify()
mapdl.prep7()

*****MAPDL VERIFICATION RUN ONLY*****
     DO NOT USE RESULTS FOR PRODUCTION

          ***** MAPDL ANALYSIS DEFINITION (PREP7) *****

Define material

Set up the material and its type (a single material, with a linking-type section and a Young’s modulus of 30e6).

mapdl.antype("STATIC")
mapdl.et(1, "LINK180")
mapdl.sectype(1, "LINK")
mapdl.secdata(1)
mapdl.mp("EX", 1, 30e6)

MATERIAL          1     EX   =  0.3000000E+08

Define geometry

Set up the nodes and elements. This creates a mesh just like in the problem setup.

mapdl.n(1, 0, 0)
mapdl.n(2, 0, 4)
mapdl.n(3, 0, 7)
mapdl.n(4, 0, 10)
mapdl.e(1, 2)
mapdl.egen(3, 1, 1)

GENERATE       3 TOTAL SETS OF ELEMENTS WITH NODE INCREMENT OF         1
   SET IS SELECTED ELEMENTS IN RANGE         1 TO         1 IN STEPS OF       1

 MAXIMUM ELEMENT NUMBER=         3

Define boundary conditions

Full constrain nodes 1 and 4, by incrementing from node 1 to node 4 in steps of 3. Apply y-direction forces to nodes 2 and 3, with values of -500 lb and -1000 lb respectively. Then exit prep7.

Effectiely, this sets: - \(F_1 = 2*F_2 = 1000 lb\)

mapdl.d(1, "ALL", "", "", 4, 3)
mapdl.f(2, "FY", -500)
mapdl.f(3, "FY", -1000)
mapdl.finish()

***** ROUTINE COMPLETED *****  CP =         0.000

Solve

Enter solution mode and solve the system.

mapdl.run("/SOLU")
out = mapdl.solve()
mapdl.finish()

FINISH SOLUTION PROCESSING


 ***** ROUTINE COMPLETED *****  CP =         0.000

Post-processing

Enter post-processing. Select the nodes at y=10 and y=0, and sum the forces there. Then store the y-components in two variables: reaction_1 and reaction_2.

mapdl.post1()
mapdl.nsel("S", "LOC", "Y", 10)
mapdl.fsum()
reaction_1 = mapdl.get("REAC_1", "FSUM", "", "ITEM", "FY")
mapdl.nsel("S", "LOC", "Y", 0)
mapdl.fsum()
reaction_2 = mapdl.get("REAC_2", "FSUM", "", "ITEM", "FY")

Check results

Now that we have the reaction forces we can compare them to the expected values of 900 lbs and 600 lbs for reactions 1 and 2 respectively.

Analytical results obtained from: - \(P = R_1 + R_2\) where \(P\) is load of 1500 lbs - \(\frac{R_2}{R_1} = \frac{a}{b}\)

Hint: Solve for each reaction force independently.

results = f"""
    ---------------------  RESULTS COMPARISON  ---------------------
    |   TARGET   |   Mechanical APDL   |   RATIO
    /INPUT FILE=    LINE=       0
    R1, lb          900.0       {abs(reaction_1)}   {abs(reaction_1) / 900}
    R2, lb          600.0       {abs(reaction_2)}   {abs(reaction_2) / 600}
    ----------------------------------------------------------------
    """
print(results)

---------------------  RESULTS COMPARISON  ---------------------
|   TARGET   |   Mechanical APDL   |   RATIO
/INPUT FILE=    LINE=       0
R1, lb          900.0       900.0   1.0
R2, lb          600.0       600.0   1.0
----------------------------------------------------------------

Stop MAPDL.

mapdl.exit()