Note
Go to the end to download the full example code.
Bending of a circular plate using axisymmetric shell elements#
- Problem description:
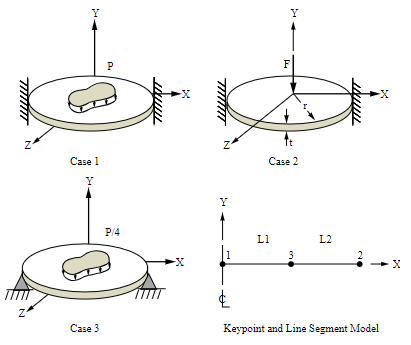
A flat circular plate of radius r and thickness t is subject to various edge constraints and surface loadings. Determine the deflection \(\delta\) at the middle and the maximum stress \(\sigma_{max}\) for each case.
Case 1: Uniform loading \(P\), clamped edge.
Case 2: Concentrated center loading \(F\), clamped edge.
Case 3: Uniform loading \(\frac{P}{4}\), simply supported edge.
- Reference:
S. Timoshenko, Strength of Materials, Part II, Elementary Theory and Problems, 3rd Edition, D. Van Nostrand Co., Inc., New York, NY, 1956, pg. 96,97, and 103.
- Analysis type(s):
Static analysis
ANTYPE=0
- Element type(s):
2-Node Finite Strain Axisymmetric Shell (SHELL208)
- Material properties:
\(E = 30 \cdot 10^6 psi\)
\(\mu = 0.3\)
- Geometric properties:
\(r = 40.0 in\)
\(t = 1.0 in\)
- Loading:
\(P = 6.0 psi\)
\(F = 7,539.82 lb\)
- Analysis assumptions and modeling notes:
The stiffness matrix formed in the first load step is automatically reused in the second load step. A new stiffness matrix is automatically formed in the third load step because of changed boundary constraints. The mesh density is biased near the centerline and outer edge to recover stress values near those points.
# sphinx_gallery_thumbnail_path = '_static/vm15_setup.png'
# Importing the `launch_mapdl` function from the `ansys.mapdl.core` module
from ansys.mapdl.core import launch_mapdl
import pandas as pd
# Launch MAPDL with specified settings
mapdl = launch_mapdl(loglevel="WARNING", print_com=True, remove_temp_dir_on_exit=True)
# Clear any existing database
mapdl.clear()
# Set the ANSYS version
mapdl.com("ANSYS MEDIA REL. 2022R2 (05/13/2022) REF. VERIF. MANUAL: REL. 2022R2")
# Run the FINISH command to exists normally from a processor
mapdl.finish()
# Run the /VERIFY command for VM15
mapdl.run("/VERIFY,VM15")
# Set the title of the analysis
mapdl.title("VM15 BENDING OF A CIRCULAR PLATE USING AXISYMMETRIC SHELL ELEMENTS")
# Enter the model creation prep7 preprocessor
mapdl.prep7(mute=True)
/COM,ANSYS MEDIA REL. 2022R2 (05/13/2022) REF. VERIF. MANUAL: REL. 2022R2
Define element type and section properties#
Use 2-Node Axisymmetric Shell (SHELL208) and include extra internal node, via Keyopt(3)=2.
mapdl.et(1, "SHELL208", "", "", 2) # Element type SHELL208
mapdl.sectype(1, "SHELL") # Section type SHELL
mapdl.secdata(1, 1) # Section data
mapdl.secnum(1) # Section number
SECTION ID NUMBER= 1
Define material#
Set up the material and its type (a single material), Young’s modulus of 30e6 and Poisson’s ratio of 0.3 is specified.
mapdl.mp("EX", 1, 30e6) # Young's modulus
mapdl.mp("NUXY", 1, 0.3) # Poisson's ratio
MATERIAL 1 NUXY = 0.3000000
Define geometry#
Set up the nodes and elements. This creates a mesh just like in the problem setup.
mapdl.n(1) # Node 1
mapdl.n(11, 40) # Node 11 at 40 degrees
mapdl.n(6, 20) # Node 6 at 20 degrees
# Generate mesh with biased elements
mapdl.fill(1, 6, 4, "", "", "", "", 20) # BIAS THE MESH TO ALLOW STRESS RECOVERY NEAR
mapdl.fill(6, 11, 4, "", "", "", "", 0.05) # THE CENTERLINE AND EDGE CONSTRAINTS
# Define element connectivity
mapdl.e(1, 2) # Element 1 with nodes 1 and 2
# Generates elements from an existing pattern
mapdl.egen(10, 1, -1)
# select all entities
mapdl.allsel()
# element plot
mapdl.eplot()
# Finish the pre-processing processor
mapdl.finish()
[82, 87, 110]
***** ROUTINE COMPLETED ***** CP = 0.000
Solve#
Enter solution mode and solve the system for three load steps.
mapdl.slashsolu()
# Set analysis type to static
mapdl.antype("STATIC")
# Controls the solution printout
mapdl.outpr("", 1)
PRINT BASI ITEMS WITH A FREQUENCY OF 1
FOR ALL APPLICABLE ENTITIES
Define boundary conditions and loadings#
Fix all degrees of freedom (dof) at node 11 and fix UX & ROTZ dofs at node 1. Solve for three load case scenarios as defined.
Case 1: Apply uniform pressure loading, P = 6 psi near clamped edge. Case 2: Concentrated center loading F = 7,539.82 lb, clamped edge. Case 3: Uniform loading P/4, simply supported edge. Then exit prep7 processor.
# Apply boundary conditions and loads for CASE 1
mapdl.d(1, "UX", "", "", "", "ROTZ") # Fix UX and ROTZ for node 1
mapdl.d(11, "ALL") # Fix all degrees of freedom for node 11
mapdl.sfe("ALL", 1, "PRES", "", 6) # Surface Pressure load = 6 PSI on all elements
# Start solve for 1st load case
mapdl.solve()
# Apply boundary conditions and loads for Load Case 2
# Load Case 2: Concentrated Center Loading - Clamped Edge
mapdl.f(1, "FY", -7539.82) # apply concentrated force FY on node 1
mapdl.sfe(
"ALL", 1, "PRES", "", 0
) # apply elemental surface pressure load of magnitude "0"
# Start solve for 2nd load case
mapdl.solve()
# Apply boundary conditions and loads for Load Case 3
# Load Case 3: Uniform Loading - Simply Supported Edge
mapdl.ddele(11, "ROTZ") # Delete clamped boundary condition constraint
mapdl.f(1, "FY") # apply nodal force of magnitude "0"
mapdl.sfe("ALL", 1, "PRES", "", 1.5) # elemental surface pressure load = 1.5 PSI
# Start solve for 3rd load case
mapdl.solve()
# exists solution processor
mapdl.finish()
FINISH SOLUTION PROCESSING
***** ROUTINE COMPLETED ***** CP = 0.000
Post-processing#
Enter post-processing. Compute deflection and stress components.
mapdl.post1()
# Set displacement scaling for post-processing
# mapdl.dscale(1, 35)
# Set up and activate window 1
mapdl.window(1, -1, 1, -1, -0.333)
# reactivates suppressed printout
mapdl.gopr()
# Set 1st load case to be read from result file for post-processing
mapdl.set(1, 1)
mapdl.pldisp(1) # Displays the displaced structure
mapdl.window(1, "OFF") # Turn off window 1
mapdl.window(2, -1, 1, -0.333, 0.333, 1) # Turn on window 2
# Don't erase existing displays
mapdl.run("/NOERASE")
NO ERASE OPTION SET
Inline functions in PyMAPDL to query node#
q = mapdl.queries
# Grab node using coordinates and assign it variable to "MID_NODE"
MID_NODE = q.node(0, 0, 0)
Retrieve nodal deflection and elemental stresses for each load cases#
# 1st load case, retrieve nodal defection UY for a node assigned to "DEF_C1"
def_c1 = mapdl.get("DEF_C1", "NODE", MID_NODE, "U", "Y")
# Define etable for elemental component stress (X)
mapdl.etable("STRS", "S", "X")
# using *get command extracting elemental stress via ETAB
strss_c1 = mapdl.get("STRSS_C1", "ELEM", 10, "ETAB", "STRS")
# Set 2nd load case to be read from result file for post-processing
mapdl.set(2, 1)
mapdl.pldisp() # Displays the displaced structure
mapdl.window(2, "OFF") # Turn off window 2
mapdl.window(3, -1, 1, 0.333, 1, 1) # Turn on window 3
# retrieve nodal defection UY for a node assigned to "DEF_C2"
def_c2 = mapdl.get("DEF_C2", "NODE", MID_NODE, "U", "Y")
# Define etable for elemental component stress (X)
mapdl.etable("STRS", "S", "X")
# using *get command extracting elemental stress via ETAB
strss_c2 = mapdl.get("STRSS_C2", "ELEM", 10, "ETAB", "STRS")
# Set 2nd load case to be read from result file for post-processing
mapdl.set(3, 1)
mapdl.pldisp() # Displays the displaced structure
# retrieve nodal defection UY for a node assigned to "DEF_C3"
def_c3 = mapdl.get("DEF_C3", "NODE", MID_NODE, "U", "Y")
# Define etable for elemental component stress (X)
mapdl.etable("STRS", "S", "X")
# using *get command extracting elemental stress via ETAB
strss_c3 = mapdl.get("STRSS_C3", "ELEM", 1, "ETAB", "STRS")
Verify the results#
# Set target values
target_def = [-0.08736, -0.08736, -0.08904]
target_strss = [7200, 3600, 2970]
# Fill result values
res_def = [def_c1, def_c2, def_c3]
res_strss = [strss_c1, strss_c2, strss_c3]
title = f"""
------------------- VM15 RESULTS COMPARISON ---------------------
"""
print(title)
col_headers = ["TARGET", "Mechanical APDL", "RATIO"]
row_headers = ["DEFLECTION (in)", "MAX STRESS (psi)"]
for lc in range(len(res_def)):
data = [
[target_def[lc], res_def[lc], abs(target_def[lc] / res_def[lc])],
[target_strss[lc], abs(res_strss[lc]), abs(target_strss[lc] / res_strss[lc])],
]
title = f"""
RESULTS FOR CASE {lc+1:1d}:
-------------------
"""
print(title)
print(pd.DataFrame(data, row_headers, col_headers))
------------------- VM15 RESULTS COMPARISON ---------------------
RESULTS FOR CASE 1:
-------------------
TARGET Mechanical APDL RATIO
DEFLECTION (in) -0.08736 -0.087641 0.996795
MAX STRESS (psi) 7200.00000 7040.372800 1.022673
RESULTS FOR CASE 2:
-------------------
TARGET Mechanical APDL RATIO
DEFLECTION (in) -0.08736 -0.088273 0.989656
MAX STRESS (psi) 3600.00000 3568.271970 1.008892
RESULTS FOR CASE 3:
-------------------
TARGET Mechanical APDL RATIO
DEFLECTION (in) -0.08904 -0.08911 0.999212
MAX STRESS (psi) 2970.00000 2966.45447 1.001195
Finish the post-processing processor#
mapdl.finish()
EXIT THE MAPDL POST1 DATABASE PROCESSOR
***** ROUTINE COMPLETED ***** CP = 0.000
Stop MAPDL#
mapdl.exit()
Total running time of the script: (0 minutes 0.856 seconds)

