Note

Go to the end to download the full example code

Bending of a Tee-Shaped Beam#

Problem description:

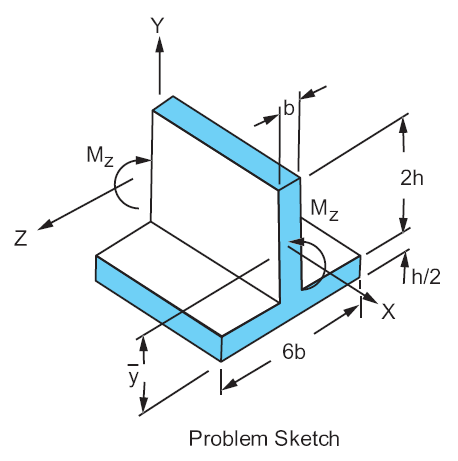
Find the maximum tensile $\sigma_{\mathrm{(B,Bot)}}$ and compressive $\sigma_{\mathrm{(B,Top)}}$ bending stresses in an unsymmetrical T-beam subjected to uniform bending $M_z$, with dimensions and geometric properties as shown below.

Reference:

S. H. Crandall, N. C. Dahl, An Introduction to the Mechanics of Solids, McGraw-Hill Book Co., Inc., New York, NY, 1959, pg. 294, ex. 7.2.

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Element Type(s):

3-D 2 Node Beam (BEAM188)

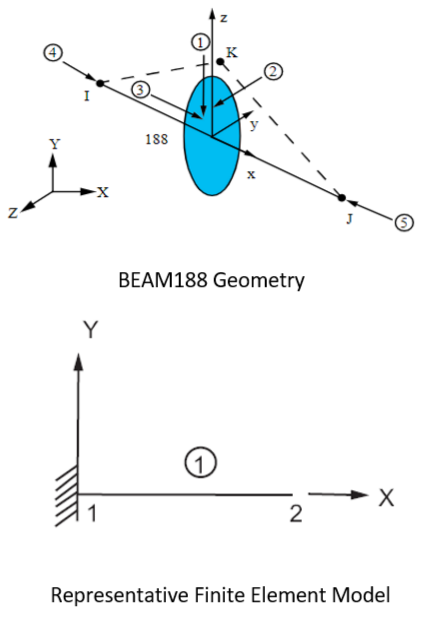
Fig. 1 **Figure 1: VM10 Geometry of Beam188 and Element Model**#

Material properties

$E = 30 \cdot 10^6 psi$
$\nu = 0.3$

Geometric Properties:

$l = 100\,in$
$h = 1.5\,in$
$b = 8\,in$

Loading:

$M_z = 100,000\,in\,lb$

Analysis Assumptions and Modeling Notes:

A length $(l = 100 in)$ is arbitrarily selected since the bending moment is constant. A T-section beam is modeled using flange width $(6b)$, flange thickness $(\frac{h}{2})$, overall depth $(2h + \frac{h}{2})$, and stem thickness $(b)$, input using Mapdl.secdata.

# sphinx_gallery_thumbnail_path = '_static/vm10_setup.png'

Start MAPDL#

Start MAPDL and import Numpy and Pandas libraries.

from ansys.mapdl.core import launch_mapdl
import numpy as np
import pandas as pd

# Start MAPDL.
mapdl = launch_mapdl()

Pre-processing#

Enter verification example mode and the pre-processing routine.

mapdl.clear()
mapdl.verify()
mapdl.prep7(mute=True)

Define element type#

Set up the element type BEAM188.

# Type of analysis: Static.
mapdl.antype("STATIC")

# Element type: BEAM188.
mapdl.et(1, "BEAM188")

# Special features are defined by keyoptions of BEAM188:

# KEYOPT(3)
# Shape functions along the length:
# Cubic
mapdl.keyopt(1, 3, 3)  # Cubic shape function

# Print the list with currently defined element types.
print(mapdl.etlist())

LIST ELEMENT TYPES FROM        1 TO        1 BY        1
   *****MAPDL VERIFICATION RUN ONLY*****
     DO NOT USE RESULTS FOR PRODUCTION

 ELEMENT TYPE        1 IS BEAM188      3-D 2-NODE BEAM
  KEYOPT( 1- 6)=        0      0      3        0      0      0
  KEYOPT( 7-12)=        0      0      0        0      0      0
  KEYOPT(13-18)=        0      0      0        0      0      0

 CURRENT NODAL DOF SET IS  UX    UY    UZ    ROTX  ROTY  ROTZ
  THREE-DIMENSIONAL MODEL

Define material#

Set up the material, where:

$E = 30 \cdot 10^6 psi$ - Young Modulus of steel.
$\nu = 0.3$ - Poisson’s ratio.

# Steel material model.
# Define Young's moulus and Poisson ratio for steel.
mapdl.mp("EX", 1, 30e6)
mapdl.mp("PRXY", 1, 0.3)

# Print the list of material properties.
print(mapdl.mplist())

LIST MATERIALS        1 TO        1 BY        1
  PROPERTY= ALL

 MATERIAL NUMBER        1

      TEMP        EX
               0.3000000E+08

      TEMP        PRXY
               0.3000000

Define section#

Set up the cross-section properties for a beam elements, where:

$w_1 = 6b = 6 \cdot 1.5 = 9\,in$ - flange width.
$w_2 = 2h + h/2 = 2 \cdot 8 + 8/2 = 20\,in$ - overall depth.
$t_1 = h/2 = 8/2 = 4\,in$ - flange thickness.
$t_2 = b = 1.5\,in$ - stem thickness.

# Parameterization of the cross-section dimensions.
sec_num = 1
w1 = 9
w2 = 20
t1 = 4
t2 = 1.5

# Define the beam cross-section.
mapdl.sectype(sec_num, "BEAM", "T")
mapdl.secdata(w1, w2, t1, t2)

# Print the section properties.
print(mapdl.slist())

*****MAPDL VERIFICATION RUN ONLY*****
     DO NOT USE RESULTS FOR PRODUCTION

 LIST SECTION ID SETS         1 TO         1 BY        1

   SECTION ID NUMBER:           1
   BEAM SECTION SUBTYPE:  T Section
   BEAM SECTION NAME IS:
   BEAM SECTION DATA SUMMARY:
    Area                 =  60.000
    Iyy                  =  2000.0
    Iyz                  =-0.47962E-13
    Izz                  =  247.50
    Warping Constant     =  673.35
    Torsion Constant     =  174.86
    Centroid  Y          = 0.14433E-15
    Centroid  Z          =  4.0000
    Shear Center Y       = 0.34916E-13
    Shear Center Z       = 0.30468
    Shear Correction-xy  = 0.54640
    Shear Correction-yz  = 0.49487E-14
    Shear Correction-xz  = 0.45475

    Beam Section is offset to CENTROID of cross section

Define geometry#

Set up the nodes and elements. Create nodes between elements.

# Define nodes for the beam element.
mapdl.n(1, x=0, y=0)
mapdl.n(2, x=100, y=0)

# Define one node for the orientation of the beam T-section.
mapdl.n(3, x=0, y=1)

# Print the list of the created nodes.
print(mapdl.nlist())

LIST ALL SELECTED NODES.   DSYS=      0
   *****MAPDL VERIFICATION RUN ONLY*****
     DO NOT USE RESULTS FOR PRODUCTION

    NODE        X             Y             Z           THXY     THYZ     THZX
        1   0.0000        0.0000        0.0000          0.00     0.00     0.00
        2   100.00        0.0000        0.0000          0.00     0.00     0.00
        3   0.0000        1.0000        0.0000          0.00     0.00     0.00

Define elements#

Create element between nodes 1 and 2 using node 3 as orientational node.

# Create element.
mapdl.e(1, 2, 3)

# Print the list of the elements and their attributes.
print(mapdl.elist())

# Display elements with their nodes numbers.
cpos = [
    (162.20508123980457, 109.41124535475498, 112.95887397446565),
    (50.0, 0.0, 0.0),
    (-0.4135015240403764, -0.4134577015789461, 0.8112146563156641),
]

mapdl.eplot(show_node_numbering=True, line_width=5, cpos=cpos, font_size=40)

LIST ALL SELECTED ELEMENTS.  (LIST NODES)
   *****MAPDL VERIFICATION RUN ONLY*****
     DO NOT USE RESULTS FOR PRODUCTION

    ELEM MAT TYP REL ESY SEC        NODES

       1   1   1   1   0   1      1     2     3

Define boundary conditions#

Application of boundary conditions (BC).

mapdl.d(node=1, lab="ALL", mute=True)
mapdl.d(node="ALL", lab="UZ", lab2="ROTX", lab3="ROTY", mute=True)

Define distributed loads#

Apply a bending moment $\mathrm{M_{z}}= 100000\,in\,lb$.

# Parametrization of the bending moment.
bending_mz = 100000

# Application of the surface load to the beam element.
mapdl.f(node=2, lab="MZ", value=bending_mz)
mapdl.finish(mute=True)

Solve#

Enter solution mode and run the simulation.

# Start solution procedure.
mapdl.slashsolu()

# Define the number of substeps to be taken this load step.
mapdl.nsubst(1)
mapdl.solve(mute=True)

Post-processing#

Enter post-processing.

# Enter the post-processing routine.
mapdl.post1(mute=True)

Getting displacements#

Using Mapdl.etable get the results of the the maximum tensile and compressive bending stresses in an unsymmetric T-beam with Mapdl.get_value.

#  Create a table of element values for BEAM188.
mapdl.etable(lab="STRS_B", item="LS", comp=1)
mapdl.etable(lab="STRS_T", item="LS", comp=31)

# Get the value of the maximum compressive stress.
strss_top_compr = mapdl.get_value(
    entity="ELEM", entnum=1, item1="ETAB", it1num="STRS_T"
)

# Get the value of the maximum tensile bending stress.
strss_bot_tens = mapdl.get_value(entity="ELEM", entnum=1, item1="ETAB", it1num="STRS_B")

Check results#

Finally we have the results of the the maximum tensile and compressive bending stresses, which can be compared with expected target values:

maximum tensile bending stress $\sigma_{\mathrm{(B,Bot)}} = 300\,psi$.
maximum compressive bending stress $\sigma_{\mathrm{(B,Top)}} = -700\,psi$.

For better representation of the results we can use pandas dataframe with following settings below:

# Define the names of the rows.
row_names = [
    "$$Stress - \sigma_{\mathrm{(B,Bot)}},\,psi$$",
    "$$Stress - \sigma_{\mathrm{(B,Top)}},\,psi$$",
]

# Define the names of the columns.
col_names = ["Target", "Mechanical APDL", "RATIO"]

# Define the values of the target results.
target_res = np.asarray([300, -700])

# Create an array with outputs of the simulations.
simulation_res = np.asarray([strss_bot_tens, strss_top_compr])

# Identifying and filling corresponding columns.
main_columns = {
    "Target": target_res,
    "Mechanical APDL": simulation_res,
    "Ratio": list(np.divide(simulation_res, target_res)),
}

# Create and fill the output dataframe with pandas.
df2 = pd.DataFrame(main_columns, index=row_names).round(1)

# Apply settings for the dataframe.
df2.head()

	Target	Mechanical APDL	Ratio
$$Stress - \sigma_{\mathrm{(B,Bot)}},\,psi$$	300	300.0	1.0
$$Stress - \sigma_{\mathrm{(B,Top)}},\,psi$$	-700	-700.0	1.0

Stop MAPDL.

mapdl.exit()

Total running time of the script: (0 minutes 0.656 seconds)

Gallery generated by Sphinx-Gallery