Note
Go to the end to download the full example code.
Force on the boundary of a semi-infinite body (Boussinesq problem)#
- Problem description:
A point force is applied at the origin of a half-space 2D axisymmetric solid modeled with far-field domain. Determine the displacement in the Y-direction on nodes along the radial direction (at location Y = 0) and vertical direction (at location X = 0).
- Reference:
TIMOSHENKO,S.P.,AND J.N.GOODIER,THEORY OF ELASTICITY MCGRAW-HILL,NEW YORK, PP 398-402, 1970.
- Analysis type(s):
Static analysis
ANTYPE=0
- Element type(s):
Structural Infinite Solid (INFIN257)
2-D 4-Node Structural Solid (PLANE182)
2-D 8-Node Structural Solid (PLANE183)
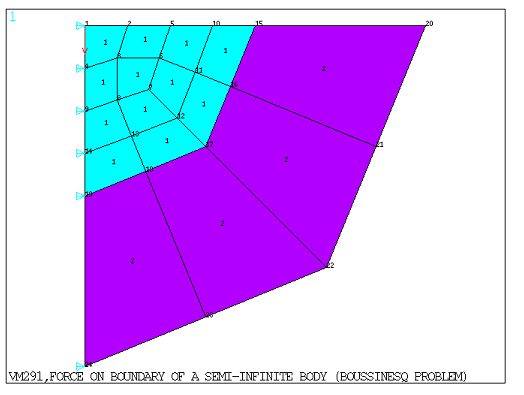
Fig. 4 PLANE182 and INFIN257#
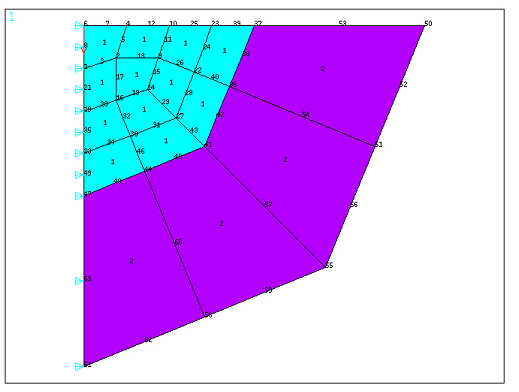
Fig. 5 PLANE183 and INFIN257#
- Material properties:
Youngs modulus, \(E = 1.0\)
Poissons ratio, \(\mu = 0.3\)
- Geometric properties:
Radius of finite mesh \(= 4.0\)
Radius of infinite mesh \(= 4.0\)
- Loading:
Point Load \(= 1.0\)
- Analysis assumptions and modeling notes:
The problem is solved for two cases: - Case 1: Using PLANE182 and INFIN257 elements - Case 2: Using PLANE183 and INFIN257 elements
The problem is composed with 12 axisymmetric finite element mesh (PLANE182 or PLANE183) with a radius of 4 from the origin, and 4 infinite element mesh (INFIN257) modeling the far-field domain with a radius of 4 extending from the finite element domain. The infinite element mesh is modeled using the EINFIN command. The UX degrees of freedom are constrained at location X = 0. The UY results are computed along the radial and vertical direction on the nodes belonging to the finite element mesh and then compared to the analytical results.
The analytic solution to compute vertical displacement for the problem of a point load on a half space is: \(\omega = \frac{P}{2 \pi E} \bigg [ \frac{(1+\nu)z^2}{(r^2+z^2)^{3/2}} + \frac{2(1-\nu ^2)}{(r^2 + z^2)^{1/2}} \bigg]\) Where \(P\) is the point load, \(E\) is the Young’s modulus, \(\nu\) is the Poisson’s ratio, and \(r\) and \(z\) are the radial and vertical distance from the point load. The above equation clearly shows the \(\frac {1}{r}\) singularity at the point of application of the load (\(r=0\) and \(z=0\)), which indicates that the finite element results may not be close to the analytical solution a points close to the origin.
# sphinx_gallery_thumbnail_path = '_static/vm291_setup1.png'
import math
# Importing the `launch_mapdl` function from the `ansys.mapdl.core` module
from ansys.mapdl.core import launch_mapdl
import numpy as np
# Launch MAPDL with specified options
mapdl = launch_mapdl(loglevel="WARNING", print_com=True, remove_temp_dir_on_exit=True)
# Clear the current database
mapdl.clear()
# Run the FINISH command to exists normally from a processor
mapdl.finish()
# Set the ANSYS version
mapdl.com("ANSYS MEDIA REL. 2022R2 (05/13/2022) REF. VERIF. MANUAL: REL. 2022R2")
# Run the /VERIFY command for VM291
mapdl.run("/VERIFY,VM291")
# Set the title of the analysis
mapdl.title("VM291 FORCE ON BOUNDARY OF A SEMI-INFINITE BODY (BOUSSINESQ PROBLEM)")
# Entering the PREP7 environment in MAPDL
mapdl.prep7(mute=True)
# Constant value of PI
pi = math.pi
/COM,ANSYS MEDIA REL. 2022R2 (05/13/2022) REF. VERIF. MANUAL: REL. 2022R2
Define element type and properties#
Use 2D 4-Node structural solid element (PLANE182) and set Keyopt(3)=1, Axisymmetric.
mapdl.et(1, "PLANE182")
mapdl.keyopt(1, 3, 1)
ELEMENT TYPE 1 IS PLANE182 4-NODE AXISYMMETRIC SOLID
KEYOPT( 1- 6)= 0 0 1 0 0 0
KEYOPT( 7-12)= 0 0 0 0 0 0
KEYOPT(13-18)= 0 0 0 0 0 0
CURRENT NODAL DOF SET IS UX UY
AXISYMMETRIC MODEL
Define material#
Set up the material and its type (a single material), Young’s modulus of 30e6 and Poisson’S ratio of 0.1 is specified.
MATERIAL 1 PRXY = 0.1000000
Define geometry#
Set up the nodes and elements. This creates a mesh just like in the problem setup.
mapdl.n(1, 0, 0)
mapdl.n(2, 1, 0)
mapdl.n(3, 0.75, -0.75)
mapdl.n(4, 0, -1)
mapdl.n(5, 2, 0)
mapdl.n(6, 1.75, -0.75)
mapdl.n(7, 1.5, -1.5)
mapdl.n(8, 0.75, -1.75)
mapdl.n(9, 0, -2)
mapdl.n(10, 3, 0)
mapdl.n(11, 2.5833, -1.0833)
mapdl.n(12, 2.1667, -2.1667)
mapdl.n(13, 1.0833, -2.5833)
mapdl.n(14, 0, -3)
mapdl.n(15, 4, 0)
mapdl.n(16, 3.4167, -1.4167)
mapdl.n(17, 2.8333, -2.8333)
mapdl.n(18, 1.4167, -3.4167)
mapdl.n(19, 0, -4)
# Define Mat =1 and Type = 1
mapdl.mat(1)
mapdl.type(1)
# FORM 2D 4 NODE STRUCTURAL SOLID ELEMENTS
mapdl.e(4, 3, 2, 1)
mapdl.e(6, 5, 2, 3)
mapdl.e(7, 6, 3, 8)
mapdl.e(9, 8, 3, 4)
mapdl.e(11, 10, 5, 6)
mapdl.e(12, 11, 6, 7)
mapdl.e(13, 12, 7, 8)
mapdl.e(14, 13, 8, 9)
mapdl.e(16, 15, 10, 11)
mapdl.e(17, 16, 11, 12)
mapdl.e(18, 17, 12, 13)
mapdl.e(19, 18, 13, 14)
12
Inline functions in PyMAPDL to query node#
Select node located at (0,0,0) and assign it to variable “NPOLE”.
SELECT ALL ENTITIES OF TYPE= ALL AND BELOW
Define boundary conditions#
Fix UX degrees of freedom at node location X=0. Apply a negative force 1.0 lb along FY direction at node 1. Then exit prep7 processor.
Effectiely, this sets: - \(Point Load = 1.0\)
# Selects nodes using location x=0
mapdl.nsel("S", "LOC", "X", 0)
# CONSTRAINT UX DOF AT LOCATION X=0
mapdl.d("ALL", "UX", 0)
# Selects all entities
mapdl.allsel()
mapdl.eplot()
# FORCE magnitude
p = -1
# APPLY FORCE ALONG Y DIRECTION AT NODE1 having magnitude "p"
mapdl.f(1, "FY", p)
# Finish pre-processing processor
mapdl.finish()
[82, 87, 110]
***** ROUTINE COMPLETED ***** CP = 0.000
Solve#
Enter solution mode and solve the system.
mapdl.slashsolu()
# Performing static analysis
mapdl.antype("STATIC")
# Controls the solution data written to the database.
mapdl.outres("ALL", "ALL")
# Sets the time for a load step, time=1
mapdl.time(1)
# SOLVE STATIC ANALYSIS
mapdl.solve()
# exists solution processor
mapdl.finish()
FINISH SOLUTION PROCESSING
***** ROUTINE COMPLETED ***** CP = 0.000
Post-processing#
Enter post-processing. Compute deflections.
mapdl.post1()
# Set the current results set to the last set to be read from result file
mapdl.set("LAST")
# redirects output to the default system output file
mapdl.run("/OUT")
# reactivates suppressed printout
mapdl.gopr()
# Set constant parameters
r1 = 1
z1 = 1
# UY AT NODE (1,0,0)
uy1 = p * (1 - nuxy**2) / (pi * exx * r1)
# UY AT NODE (0,1,0)
up1 = p / (2 * pi * exx * z1) * (1 + nuxy + 2 - 2 * nuxy**2)
# MAPDL UY AT NODE(1,0,0)
uya1 = mapdl.get("UYA1", "NODE", 2, "U", "Y")
# MADPL UY AT NODE(0,1,0)
upa1 = mapdl.get("UPA1", "NODE", 4, "U", "Y")
# Set constant parameters
r2 = 2
z2 = 2
# UY AT NODE (2,0,0)
uy2 = p * (1 - nuxy**2) / (pi * exx * r2)
# UY AT NODE (0,2,0)
up2 = p / (2 * pi * exx * z2) * (1 + nuxy + 2 - 2 * nuxy**2)
# MAPDL UY AT NODE(2,0,0)
uya2 = mapdl.get("UYA2", "NODE", 5, "U", "Y")
# MADPL UY AT NODE(0,2,0)
upa2 = mapdl.get("UPA2", "NODE", 9, "U", "Y")
# Set constant parameters, R3=3 and Z3=3
r3 = 3
z3 = 3
# UY AT NODE (3,0,0)
uy3 = p * (1 - nuxy**2) / (pi * exx * r3)
# UY AT NODE (0,3,0)
up3 = p / (2 * pi * exx * z3) * (1 + nuxy + 2 - 2 * nuxy**2)
# MAPDL UY AT NODE(3,0,0)
uya3 = mapdl.get("UYA3", "NODE", 10, "U", "Y")
# MADPL UY AT NODE(0,3,0)
upa3 = mapdl.get("UPA3", "NODE", 14, "U", "Y")
# Set constant parameters, R4=4 and Z4=4
r4 = 4
z4 = 4
# UY AT NODE (4,0,0)
uy4 = p * (1 - nuxy**2) / (pi * exx * r4)
# UY AT NODE (0,4,0)
up4 = p / (2 * pi * exx * z4) * (1 + nuxy + 2 - 2 * nuxy**2)
# MAPDL UY AT NODE(4,0,0)
uya4 = mapdl.get("UYA4", "NODE", 15, "U", "Y")
# MADPL UY AT NODE(0,4,0)
upa4 = mapdl.get("UPA4", "NODE", 19, "U", "Y")
# assign labels for nodes
label1 = np.array(["NODE5", "NODE10", "NODE15"])
label2 = np.array(["NODE9", "NODE14", "NODE19"])
# create results arrays for printout
value1 = np.array([uy2, uy3, uy4])
value_ana1 = np.array([uya2, uya3, uya4])
value_ratio1 = []
for i in range(len(value_ana1)):
a = value1[i] / value_ana1[i]
value_ratio1.append(a)
# create results arrays for printout
value2 = np.array([up2, up3, up4])
value_ana2 = np.array([upa2, upa3, upa4])
value_ratio2 = []
for i in range(len(value_ana2)):
a = value2[i] / value_ana2[i]
value_ratio2.append(a)
Verify the results#
results = f"""
--------------------------VM291 RESULTS COMPARISON--------------------------
USING PLANE182 AND INFIN257 ELEMENTS
-------------------------------------
VERTICAL DISPLACEMENT(UY) ON THE SURFACE (Y=0)
----------------------------------------------
| NODES | TARGET | Mechanical APDL | RATIO
"""
print(results)
for i in range(len(value1)):
message = f"""
{label1[i]} {value1[i]:.5f} {value_ana1[i]:.5f} {value_ratio1[i]:.5f}
"""
print(message)
results = f"""
VERTICAL DISPLACEMENT(UY) BELOW THE POINT LOAD (X=0)
----------------------------------------------------
"""
print(results)
for i in range(len(value2)):
message = f"""
{label2[i]} {value2[i]:.5f} {value_ana2[i]:.5f} {value_ratio2[i]:.5f}
"""
print(message)
--------------------------VM291 RESULTS COMPARISON--------------------------
USING PLANE182 AND INFIN257 ELEMENTS
-------------------------------------
VERTICAL DISPLACEMENT(UY) ON THE SURFACE (Y=0)
----------------------------------------------
| NODES | TARGET | Mechanical APDL | RATIO
NODE5 -0.15756 -0.15037 1.04786
NODE10 -0.10504 -0.10090 1.04110
NODE15 -0.07878 -0.07714 1.02128
VERTICAL DISPLACEMENT(UY) BELOW THE POINT LOAD (X=0)
----------------------------------------------------
NODE9 -0.24510 -0.23512 1.04246
NODE14 -0.16340 -0.16882 0.96791
NODE19 -0.12255 -0.12920 0.94855
Finish the post-processing processor#
mapdl.finish()
EXIT THE MAPDL POST1 DATABASE PROCESSOR
***** ROUTINE COMPLETED ***** CP = 0.000
Clears the database without restarting#
Define material#
Set up the material and its type (a single material), Young’s modulus of 30e6 and Poisson’S ratio of 0.1 is specified.
MATERIAL 1 PRXY = 0.1000000
Define element type and properties#
Use 2D 8-Node structural solid element (PLANE183) and set Keyopt(3)=1, Axisymmetric.
mapdl.et(1, "PLANE183")
mapdl.keyopt(1, 3, 1)
ELEMENT TYPE 1 IS PLANE183 8-NODE AXISYMMETRIC SOLID
KEYOPT( 1- 6)= 0 0 1 0 0 0
KEYOPT( 7-12)= 0 0 0 0 0 0
KEYOPT(13-18)= 0 0 0 0 0 0
CURRENT NODAL DOF SET IS UX UY
AXISYMMETRIC MODEL
Define geometry#
Set up the nodes and elements. This creates a mesh just like in the problem setup.
mapdl.n(1, 0.0000, -1.0000, 0.0000)
mapdl.n(2, 0.75000, -0.75000, 0.0000)
mapdl.n(3, 0.37500, -0.87500, 0.0000)
mapdl.n(4, 1.0000, 0.0000, 0.0000)
mapdl.n(5, 0.87500, -0.37500, 0.0000)
mapdl.n(6, 0.0000, 0.0000, 0.0000)
mapdl.n(7, 0.50000, 0.0000, 0.0000)
mapdl.n(8, 0.0000, -0.50000, 0.0000)
mapdl.n(9, 1.7500, -0.75000, 0.0000)
mapdl.n(10, 2.0000, 0.0000, 0.0000)
mapdl.n(11, 1.8750, -0.37500, 0.0000)
mapdl.n(12, 1.5000, 0.0000, 0.0000)
mapdl.n(13, 1.2500, -0.75000, 0.0000)
mapdl.n(14, 1.5000, -1.5000, 0.0000)
mapdl.n(15, 1.6250, -1.1250, 0.0000)
mapdl.n(16, 0.75000, -1.7500, 0.0000)
mapdl.n(17, 0.75000, -1.2500, 0.0000)
mapdl.n(18, 1.1250, -1.6250, 0.0000)
mapdl.n(19, 0.0000, -2.0000, 0.0000)
mapdl.n(20, 0.37500, -1.8750, 0.0000)
mapdl.n(21, 0.0000, -1.5000, 0.0000)
mapdl.n(22, 2.5833, -1.0833, 0.0000)
mapdl.n(23, 3.0000, 0.0000, 0.0000)
mapdl.n(24, 2.7917, -0.54165, 0.0000)
mapdl.n(25, 2.5000, 0.0000, 0.0000)
mapdl.n(26, 2.1667, -0.91665, 0.0000)
mapdl.n(27, 2.1667, -2.1667, 0.0000)
mapdl.n(28, 2.3750, -1.6250, 0.0000)
mapdl.n(29, 1.8334, -1.8334, 0.0000)
mapdl.n(30, 1.0833, -2.5833, 0.0000)
mapdl.n(31, 1.6250, -2.3750, 0.0000)
mapdl.n(32, 0.91665, -2.1667, 0.0000)
mapdl.n(33, 0.0000, -3.0000, 0.0000)
mapdl.n(34, 0.54165, -2.7917, 0.0000)
mapdl.n(35, 0.0000, -2.5000, 0.0000)
mapdl.n(36, 3.4167, -1.4167, 0.0000)
mapdl.n(37, 4.0000, 0.0000, 0.0000)
mapdl.n(38, 3.7083, -0.70835, 0.0000)
mapdl.n(39, 3.5000, 0.0000, 0.0000)
mapdl.n(40, 3.0000, -1.2500, 0.0000)
mapdl.n(41, 2.8333, -2.8333, 0.0000)
mapdl.n(42, 3.1250, -2.1250, 0.0000)
mapdl.n(43, 2.5000, -2.5000, 0.0000)
mapdl.n(44, 1.4167, -3.4167, 0.0000)
mapdl.n(45, 2.1250, -3.1250, 0.0000)
mapdl.n(46, 1.2500, -3.0000, 0.0000)
mapdl.n(47, 0.0000, -4.0000, 0.0000)
mapdl.n(48, 0.70835, -3.7083, 0.0000)
mapdl.n(49, 0.0000, -3.5000, 0.0000)
# Define Mat =1 and Type = 1
mapdl.mat(1)
mapdl.type(1)
# DEFINE ELEMENTS
mapdl.e(1, 2, 4, 6, 3, 5, 7, 8)
mapdl.e(9, 10, 4, 2, 11, 12, 5, 13)
mapdl.e(14, 9, 2, 16, 15, 13, 17, 18)
mapdl.e(19, 16, 2, 1, 20, 17, 3, 21)
mapdl.e(22, 23, 10, 9, 24, 25, 11, 26)
mapdl.e(27, 22, 9, 14, 28, 26, 15, 29)
mapdl.e(30, 27, 14, 16, 31, 29, 18, 32)
mapdl.e(33, 30, 16, 19, 34, 32, 20, 35)
mapdl.e(36, 37, 23, 22, 38, 39, 24, 40)
mapdl.e(41, 36, 22, 27, 42, 40, 28, 43)
mapdl.e(44, 41, 27, 30, 45, 43, 31, 46)
mapdl.e(47, 44, 30, 33, 48, 46, 34, 49)
12
Inline functions in PyMAPDL to query node#
Select node located at (0,0,0) and assign it to variable “NPOLE”.
q = mapdl.queries
NPOLE = q.node(0, 0, 0)
# select nodes
mapdl.nsel("S", "NODE", "", 36, 38, 1)
mapdl.nsel("A", "NODE", "", 41, 42, 1)
mapdl.nsel("A", "NODE", "", 44, 45, 1)
mapdl.nsel("A", "NODE", "", 47, 48, 1)
# GENERATE SEMI-INFINITE SOLID ELEMENTS
mapdl.einfin("", NPOLE)
# Selects all entities
mapdl.allsel()
mapdl.eplot()
[82, 87, 110]
Define boundary conditions#
Fix UX degrees of freedom at node location X=0. Apply a negative force 1.0 lb along FY direction at node 6. Then exit prep7 processor.
Effectiely, this sets: - \(Point Load = 1.0\)
***** ROUTINE COMPLETED ***** CP = 0.000
Solve#
Enter solution mode and solve the system.
mapdl.slashsolu()
# Performing static analysis
mapdl.antype("STATIC")
# Controls the solution data written to the database.
mapdl.outres("ALL", "ALL")
# Sets the time for a load step, time=1
mapdl.time(1)
# SOLVE STATIC ANALYSIS
mapdl.solve()
# exists solution processor
mapdl.finish()
FINISH SOLUTION PROCESSING
***** ROUTINE COMPLETED ***** CP = 0.000
Post-processing#
Enter post-processing. Compute deflections.
mapdl.post1()
# Set the current results set to the last set to be read from result file
mapdl.set("LAST")
# redirects output to the default system output file
mapdl.run("/OUT")
# reactivates suppressed printout
mapdl.gopr()
# Set constant parameters
r1 = 1
z1 = 1
# UY AT NODE (1,0,0)
uy1 = p * (1 - nuxy**2) / (pi * exx * r1)
# UY AT NODE (0,1,0)
up1 = p / (2 * pi * exx * z1) * (1 + nuxy + 2 - 2 * nuxy**2)
# MAPDL UY AT NODE(1,0,0)
uya1 = mapdl.get("UYA1", "NODE", 4, "U", "Y")
# MADPL UY AT NODE(0,1,0)
upa1 = mapdl.get("UPA1", "NODE", 1, "U", "Y")
# Set constant parameters
r2 = 2
z2 = 2
# UY AT NODE (2,0,0)
uy2 = p * (1 - nuxy**2) / (pi * exx * r2)
# UY AT NODE (0,2,0)
up2 = p / (2 * pi * exx * z2) * (1 + nuxy + 2 - 2 * nuxy**2)
# MAPDL UY AT NODE(2,0,0)
uya2 = mapdl.get("UYA2", "NODE", 10, "U", "Y")
# MADPL UY AT NODE(0,2,0)
upa2 = mapdl.get("UPA2", "NODE", 19, "U", "Y")
# Set constant parameters
r3 = 3
z3 = 3
# UY AT NODE (3,0,0)
uy3 = p * (1 - nuxy**2) / (pi * exx * r3)
# UY AT NODE (0,3,0)
up3 = p / (2 * pi * exx * z3) * (1 + nuxy + 2 - 2 * nuxy**2)
# MAPDL UY AT NODE(3,0,0)
uya3 = mapdl.get("UYA3", "NODE", 23, "U", "Y")
# MADPL UY AT NODE(0,3,0)
upa3 = mapdl.get("UPA3", "NODE", 33, "U", "Y")
# Set constant parameters
r4 = 4
z4 = 4
# UY AT NODE (4,0,0)
uy4 = p * (1 - nuxy**2) / (pi * exx * r4)
# UY AT NODE (0,4,0)
up4 = p / (2 * pi * exx * z4) * (1 + nuxy + 2 - 2 * nuxy**2)
# MAPDL UY AT NODE(4,0,0)
uya4 = mapdl.get("UYA4", "NODE", 37, "U", "Y")
# MADPL UY AT NODE(0,4,0)
upa4 = mapdl.get("UPA4", "NODE", 47, "U", "Y")
# Assign labels for nodes
label1 = np.array(["NODE10", "NODE23", "NODE37"])
label2 = np.array(["NODE19", "NODE33", "NODE47"])
# Create results arrays for printout
value1 = np.array([uy2, uy3, uy4])
value_ana1 = np.array([uya2, uya3, uya4])
value_ratio1 = []
for i in range(len(value_ana1)):
a = value1[i] / value_ana1[i]
value_ratio1.append(a)
# Create results arrays for printout
value2 = np.array([up2, up3, up4])
value_ana2 = np.array([upa2, upa3, upa4])
value_ratio2 = []
for i in range(len(value_ana2)):
a = value2[i] / value_ana2[i]
value_ratio2.append(a)
mapdl.gopr()
results = f"""
USING PLANE183 AND INFIN257 ELEMENTS
------------------------------------
VERTICAL DISPLACEMENT(UY) ON THE SURFACE (Y=0)
----------------------------------------------
"""
print(results)
for i in range(len(value1)):
message = f"""
{label1[i]} {value1[i]:.5f} {value_ana1[i]:.5f} {value_ratio1[i]:.5f}
"""
print(message)
results = f"""
VERTICAL DISPLACEMENT(UY) BELOW THE POINT LOAD (X=0)
----------------------------------------------------
"""
print(results)
for i in range(len(value2)):
message = f"""
{label2[i]} {value2[i]:.5f} {value_ana2[i]:.5f} {value_ratio2[i]:.5f}
"""
print(message)
message = f"""
-----------------------------------------------------------------
"""
print(message)
USING PLANE183 AND INFIN257 ELEMENTS
------------------------------------
VERTICAL DISPLACEMENT(UY) ON THE SURFACE (Y=0)
----------------------------------------------
NODE10 -0.15756 -0.15745 1.00070
NODE23 -0.10504 -0.10582 0.99264
NODE37 -0.07878 -0.07865 1.00162
VERTICAL DISPLACEMENT(UY) BELOW THE POINT LOAD (X=0)
----------------------------------------------------
NODE19 -0.24510 -0.26633 0.92029
NODE33 -0.16340 -0.16186 1.00952
NODE47 -0.12255 -0.12254 1.00010
-----------------------------------------------------------------
Finish the post-processing processor#
mapdl.finish()
EXIT THE MAPDL POST1 DATABASE PROCESSOR
***** ROUTINE COMPLETED ***** CP = 0.000
Stop MAPDL#
mapdl.exit()
Total running time of the script: (0 minutes 1.622 seconds)

