Residual Stress Problem

Problem description:

• A chain hoist is attached to the ceiling through three tie rods as shown below. The tie rods are made of cold-rolled steel with yield strength \(\sigma_{yp}\) and each has an area A. Find the deflection \(\delta\) at load \(F_1\) when the deflections are elastic in all three rods. When the frame is loaded to \(F_2\) (where all three rods become fully plastic), and then unloaded, find the residual stress \(\sigma_r\) in the central rod.

Reference:

• S. H. Crandall, N. C. Dahl, An Introduction to the Mechanics of Solids, McGraw-Hill Book Co., Inc., New York, NY, 1959, pg. 234, problem 5.31.

Analysis Type(s):

• Static Analysis (ANTYPE = 0)

Element Type(s):

• 3-D Spar (or Truss) Elements (LINK180)

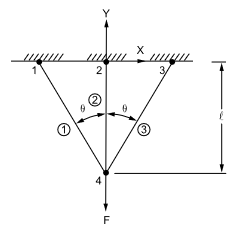
Fig. 2 VM11 Problem model

Material properties

• \(\sigma_{yp} = 30,000\,psi\)

• \(E = 30 \cdot 10^6\,psi\)

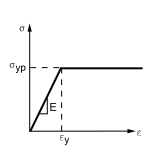
Fig. 3 VM11 Material Model

Geometric Properties:

• \(A = 1\,in^2\)

• \(l = 100\,in\)

• \(\Theta = 30°\)

Loading:

• \(F_1 = 51,961.5\,lb\)

• \(F_2 = 81,961.5\,lb\)

Analysis Assumptions and Modeling Notes:

• Automatic load stepping (:meth: Mapl.autots <ansys.mapdl.core.Mapdl.autots>,ON) is used to obtain the nonlinear plastic solution (load steps 2 and 3).

# sphinx_gallery_thumbnail_path = '_static/vm11_setup_1.png'

import math

from ansys.mapdl.core import launch_mapdl

Start MAPDL

Start MAPDL.

mapdl = launch_mapdl()
mapdl.clear()  # optional as MAPDL just started

Pre-processing

Enter verification example mode and the pre-processing routine.

mapdl.verify("vm11")
mapdl.prep7()
mapdl.title("VM11 RESIDUAL STRESS PROBLEM", mute=True)

Define element type

Set up the element type LINK180.

# Type of analysis: Static.
mapdl.antype("STATIC")

# Element type: LINK180.
mapdl.et(1, "LINK180")
mapdl.sectype(1, "LINK")
mapdl.secdata(1)
mapdl.mp("EX", 1, 30e6)
mapdl.tb("PLAS", 1, tbopt="BKIN")  # TABLE FOR BILINEAR KINEMATIC HARDENING
mapdl.tbtemp(100)
mapdl.tbdata(1, 30000)  # YIELD STRESS

# Print
print(mapdl.mplist())

LIST MATERIALS        1 TO        1 BY        1
  PROPERTY= ALL

 MATERIAL NUMBER        1

      TEMP        EX
               0.3000000E+08

Define model geometry

Set up parameters and geometry.

L = 100
theta = 30
xloc = L * math.tan(math.radians(theta))
mapdl.n(1, -xloc)
mapdl.n(3, xloc)
mapdl.fill()
mapdl.n(4, y=-L, mute=True)

Define elements

Create elements.

mapdl.e(1, 4)
mapdl.e(2, 4)
mapdl.e(3, 4)
mapdl.outpr(freq=1)
mapdl.d(1, "ALL", nend=3)
mapdl.f(4, "FY", -51961.5)  # APPLY LOAD F1
mapdl.finish(mute=True)
mapdl.eplot()

Solve

Enter solution mode and run the simulation.

mapdl.slashsolu()
mapdl.solve()
mapdl.finish(mute=True)

Post-processing

Enter post-processing.

# Enter the post-processing routine.
mapdl.post1()

q = mapdl.queries
bot_node = q.node(0, -100, 0)
def_node = mapdl.get_value("NODE", bot_node, "U", "Y")
mapdl.finish()
mapdl.slashsolu()
mapdl.autots("ON")  # TURN ON AUTOMATIC LOAD STEPPING
mapdl.nsubst(10)
mapdl.outpr(freq=10)
mapdl.f(4, "FY", -81961.5)  # APPLY LOAD F2
mapdl.solve()
mapdl.nsubst(5)
mapdl.outpr(freq=5)
mapdl.fdele(4, "FY")  # REMOVE LOAD F2
mapdl.solve()
mapdl.finish()


mapdl.post1()
mapdl.etable("STRS", "LS", 1)
strss = mapdl.get_value("ELEM", 2, "ETAB", "STRS")
message = f"""
------------------- VM11 RESULTS COMPARISON ---------------------
   TARGET      |  TARGET     |   ANSYS       |   RATIO
Def at F1 (in)   {-0.07533:.5f}        {def_node:.5f}      {abs(def_node/0.07533):.5f}
Stress (psi)     {-5650:.5f}     {strss:.5f}   {abs(strss/-5650):.5f}
-----------------------------------------------------------------
"""
print(message)

mapdl.finish()

------------------- VM11 RESULTS COMPARISON ---------------------
   TARGET      |  TARGET     |   ANSYS       |   RATIO
Def at F1 (in)   -0.07533        -0.07534      1.00011
Stress (psi)     -5650.00000     -5650.34424   1.00006
-----------------------------------------------------------------


EXIT THE MAPDL POST1 DATABASE PROCESSOR


 ***** ROUTINE COMPLETED *****  CP =         0.000

Stop MAPDL.

mapdl.exit()