Parametric calculation

Problem description:

• Write a user file macro to calculate the distance d between either nodes or keypoints in PREP7. Define abbreviations for calling the macro and verify the parametric expressions by using the macro to calculate the distance between nodes \(N_1\) and \(N_2\) and between keypoints \(K_3\) and \(K_4\).

Reference:

• None.

Analysis type(s):

• Parametric arithmetic.

Element type:

• None.

Geometric properties (coordinates):

• \(N_{\mathrm{1(x,y,z)}} = 1.5, 2.5, 3.5\)

• \(N_{\mathrm{2(x,y,z)}} = -3.7, 4.6, -3\)

• \(K_{\mathrm{3(x,y,z)}} = 100, 0, 30\)

• \(K_{\mathrm{4(x,y,z)}} = -200,25,80\)

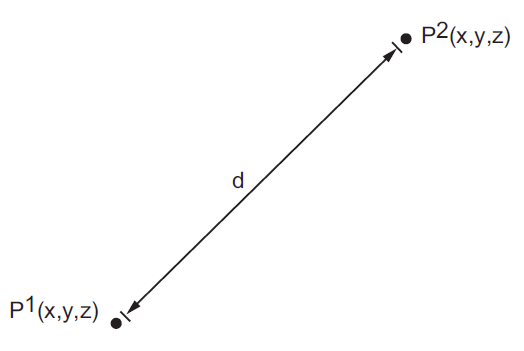
Analysis assumptions and modeling notes:

• Instead of *CREATE, *USE, etc., we have created a class Create with methods that correspond to each type of simulation. This class gives a possibility to change coordinates and reuse it. The simulation can be checked not just by target values, but also with the simple distances’ formula between keypoints as:

  • Calculate distance between two keypoints in the Cartesian coordinate system:

    \(D = \sqrt[2]{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}\)

  • Python representation of the distance formula:

    import math
    # Define coordinates for keypoints K3 and K4.
    x1, y1, z1 = 100, 0, 30
    x2, y2, z2 = -200, 25, 80
    dist_kp = math.sqrt((x2 - x1)**2 + (y2 - y1)**2 + (z2 - z1)**2)
    print(dist_kp)
    

# sphinx_gallery_thumbnail_path = '_static/vm8_setup.png'

Start MAPDL

Start MAPDL and import Numpy and Pandas libraries.

from ansys.mapdl.core import launch_mapdl
import numpy as np
import pandas as pd

# Start MAPDL.
mapdl = launch_mapdl()

Pre-processing

Enter verification example mode and the pre-processing routine.

mapdl.clear()
mapdl.verify()
mapdl.prep7(mute=True)

Define class

Identifying the class create with methods create_kp_method and create_node_method to calculate and plot the distances between keypoints and nodes.

class Create:
    def __init__(self, p1, p2):
        # Points Attributes.
        self.p1 = p1
        self.p2 = p2

    def kp_distances(self):

        # Define keypoints by coordinates.
        kp1 = mapdl.k(npt=3, x=self.p1[0], y=self.p1[1], z=self.p1[2])
        kp2 = mapdl.k(npt=4, x=self.p2[0], y=self.p2[1], z=self.p2[2])

        # Get the distance between keypoints.
        dist_kp, kx, ky, kz = mapdl.kdist(kp1, kp2)

        # Plot keypoints.
        mapdl.kplot(
            show_keypoint_numbering=True,
            vtk=True,
            background="grey",
            show_bounds=True,
            font_size=26,
        )
        return dist_kp

    def node_distances(self):

        # Define nodes by coordinates.
        node1 = mapdl.n(node=1, x=self.p1[0], y=self.p1[1], z=self.p1[2])
        node2 = mapdl.n(node=2, x=self.p2[0], y=self.p2[1], z=self.p2[2])

        # Get the distance between nodes.
        dist_node, node_x, node_y, node_z = mapdl.ndist(node1, node2)

        # Plot nodes.
        mapdl.nplot(nnum=True, vtk=True, color="grey", show_bounds=True, font_size=26)
        return dist_node

    @property
    def p1(self):
        # Getting value
        return self._p1

    @p1.setter
    def p1(self, new_value):
        # Check the data type:
        if not isinstance(new_value, list):
            raise ValueError("The coordinates should be implemented by the list!")
        # Check the quantity of items:
        if len(new_value) != 3:
            raise ValueError(
                "The coordinates should have three items in the list as [X, Y, Z]"
            )
        self._p1 = new_value

    @property
    def p2(self):
        return self._p2

    @p2.setter
    def p2(self, new_value):
        # Check the data type:
        if not isinstance(new_value, list):
            raise ValueError("The coordinates should be implemented by the list!")
        # Check the quantity of items:
        if len(new_value) != 3:
            raise ValueError(
                "The coordinates should have three items in the list as [X, Y, Z]"
            )
        self._p2 = new_value

Distance between keypoints

Using already created method for keypoints to get the distance between them and print out an output. The keypoints have got next coordinates:

• \(K_{\mathrm{3(x,y,z)}} = 100, 0, 30\)

• \(K_{\mathrm{4(x,y,z)}} = -200, 25,80\)

kp1 = [100, 0, 30]
kp2 = [-200, 25, 80]
kp = Create(kp1, kp2)
kp_dist = kp.kp_distances()
print(f"Distance between keypoint is: {kp_dist:.2f}\n\n")

# Print the list of keypoints.
print(mapdl.klist())

Static Scene

Interactive Scene

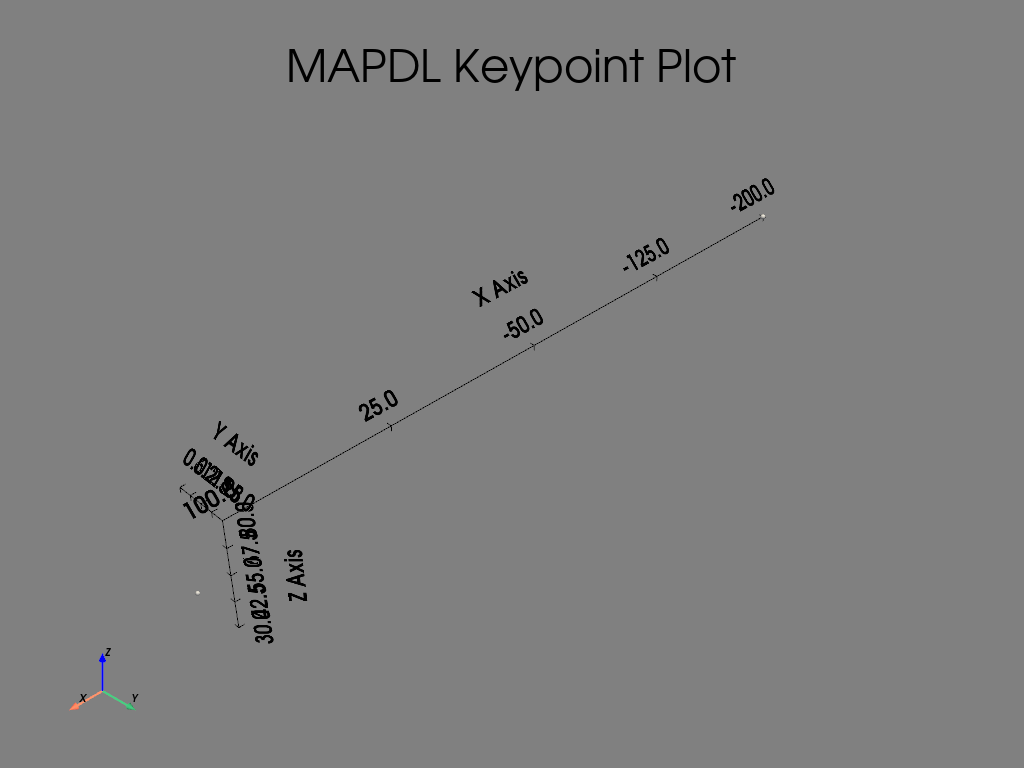
Distance between keypoint is: 305.16


LIST ALL SELECTED KEYPOINTS.   DSYS=      0
   *****MAPDL VERIFICATION RUN ONLY*****
     DO NOT USE RESULTS FOR PRODUCTION

    NO. X,Y,Z LOCATION                   KESIZE     NODE  ELEM MAT REAL TYP ESYS
     3   100.       0.00       30.0       0.00         0     0   0    0   0    0
     4  -200.       25.0       80.0       0.00         0     0   0    0   0    0

Distance between nodes.

Using already created method for nodes to get the distance between them and print out an output. The nodes have got next coordinates:

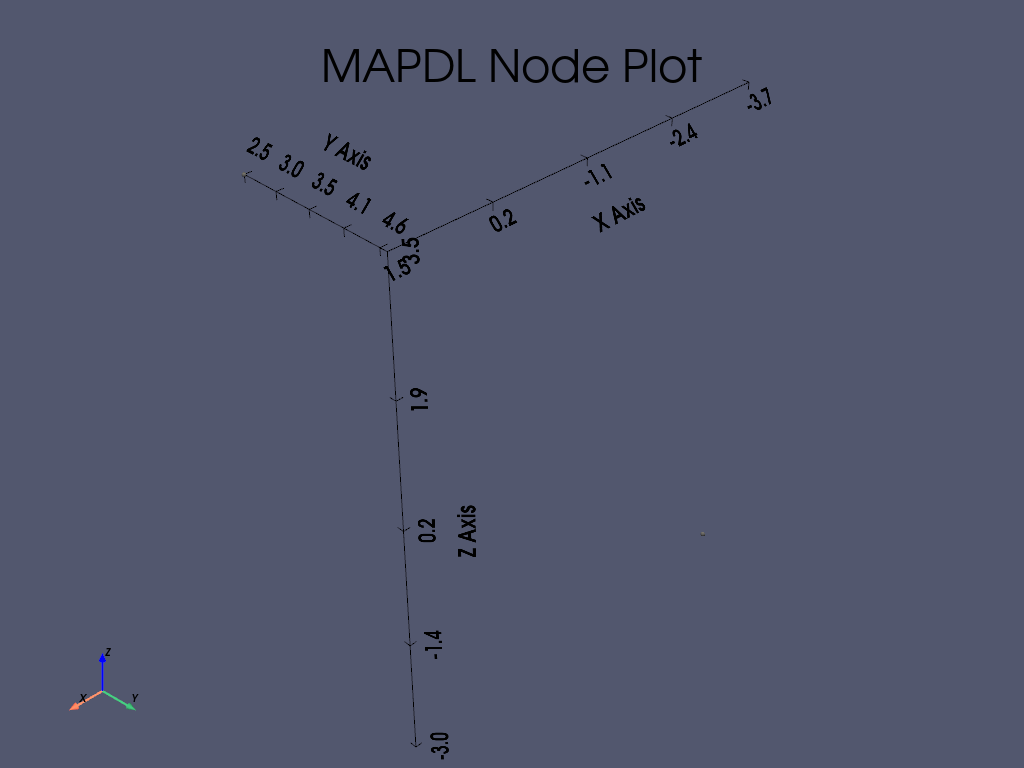
• \(N_{\mathrm{1(x,y,z)}} = 1.5, 2.5, 3.5\)

• \(N_{\mathrm{2(x,y,z)}} = -3.7, 4.6, -3\)

node1 = [1.5, 2.5, 3.5]
node2 = [-3.7, 4.6, -3]
nodes = Create(node1, node2)
node_dist = nodes.node_distances()
print(f"Distance between nodes is: {node_dist:.2f}\n\n")

# Print the list of nodes.
print(mapdl.nlist())

Static Scene

Interactive Scene

[82, 87, 110]
Distance between nodes is: 8.58


LIST ALL SELECTED NODES.   DSYS=      0
   *****MAPDL VERIFICATION RUN ONLY*****
     DO NOT USE RESULTS FOR PRODUCTION

    NODE        X             Y             Z           THXY     THYZ     THZX
        1   1.5000        2.5000        3.5000          0.00     0.00     0.00
        2  -3.7000        4.6000       -3.0000          0.00     0.00     0.00

Check results

Finally we have the results of the distances for both simulations, which can be compared with expected target values:

• 1st simulation to get the distance between keypoints \(K_3\) and \(K_4\), where \(LEN_1 = 305.16\,(in)\)

• 2nd simulation to get the distance between nodes \(N_1\) and \(N_2\), where \(LEN_2 = 8.58\,(in)\)

For better representation of the results we can use pandas dataframe with following settings below:

# Define the names of the rows.
row_names = ["N1 - N2 distance (LEN2)", "K3 - K4 distance (LEN1)"]

# Define the names of the columns.
col_names = ["Target", "Mechanical APDL", "RATIO"]

# Define the values of the target results.
target_res = np.asarray([8.5849, 305.16])

# Create an array with outputs of the simulations.
simulation_res = np.asarray([node_dist, kp_dist])

# Identifying and filling corresponding columns.
main_columns = {
    "Target": target_res,
    "Mechanical APDL": simulation_res,
    "Ratio": list(np.divide(simulation_res, target_res)),
}

# Create and fill the output dataframe with pandas.
df2 = pd.DataFrame(main_columns, index=row_names).round(2)

# Apply settings for the dataframe.
df2.head()

	Target	Mechanical APDL	Ratio
N1 - N2 distance (LEN2)	8.58	8.58	1.0
K3 - K4 distance (LEN1)	305.16	305.16	1.0

Stop MAPDL.

mapdl.exit()