Large Deflection Eccentric Compression of Slender Column

Problem description:

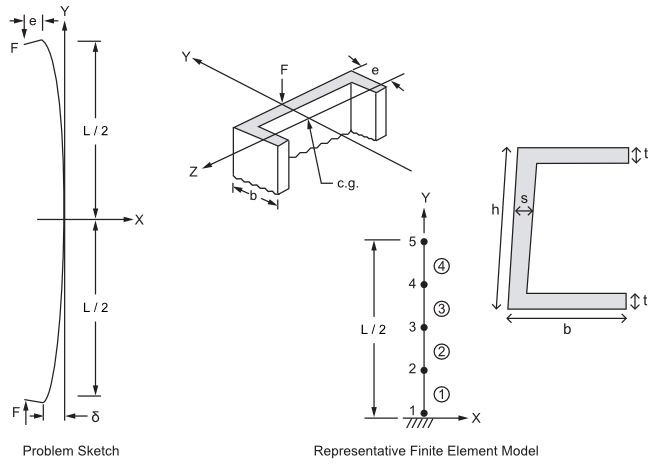
• Find the deflection \(\delta\) at the middle and the maximum tensile and compressive stresses in an eccentrically compressed steel strut of length L. The cross-section is a channel with the dimensions shown in the diagram. The ends are pinned at the point of load application. The distance between the centroid and the back of the channel is e, and the compressive force F acts in the plane of the back of the channel and in the symmetry plane of the channel.

Reference:

• S. Timoshenko, Strength of Materials, Part I, Elementary Theory and Problems, 3rd Edition, D. Van Nostrand Co., Inc., New York, NY, 1955, pg. 263, problem 1.

Analysis type(s):

• Static, Large Deflection Analysis ANTYPE=0

Element type(s):

• Elastic Tapered Unsymmetric Beam Elements (BEAM188)

Material properties:

• \(E = 30 \cdot 10^6 psi\)

• \(\mu = 0.3\)

Geometric properties:

• \(L = 10 ft\)

• \(h = 8 in\)

• \(s = 0.22 in\)

• \(t = 0.39 in\)

• \(e = 0.6465 in\)

• \(b = 2.26 in\)

Loading:

• \(F = 4000 lb\)

Analysis Assumptions and Modeling Notes:

• Only one-half of the structure is modeled because of symmetry. The boundary conditions for the equivalent half model become fixed-free. Large deflection is needed since the stiffness of the structure and the loading change significantly with deflection. The offset e is defined in the element coordinate system.

# sphinx_gallery_thumbnail_path = '_static/vm14_setup.png'

# Importing the `launch_mapdl` function from the `ansys.mapdl.core` module
from ansys.mapdl.core import launch_mapdl
import pandas

# Launch MAPDL with specified settings
mapdl = launch_mapdl(loglevel="WARNING", print_com=True, remove_temp_dir_on_exit=True)

# Clear any existing database
mapdl.clear()

# Set the ANSYS version
mapdl.com("ANSYS MEDIA REL. 2022R2 (05/13/2022) REF. VERIF. MANUAL: REL. 2022R2")

# Run the FINISH command to exists normally from a processor
mapdl.finish()

# Run the /VERIFY command for VM14
mapdl.run("/VERIFY,VM14")

# Set the title of the analysis
mapdl.title("VM14 LARGE DEFLECTION ECCENTRIC COMPRESSION OF SLENDER COLUMN")

# Enter the model creation preprocessor
mapdl.prep7(mute=True)

Define element type and properties

Use 3D 2-Node Beam element (Beam188) and set cubic shape function Keyopt(3)=3.

mapdl.et(1, "BEAM188", "", "", 3)  # Element type BEAM188
mapdl.sectype(1, "BEAM", "CHAN")  # Section type BEAM CHAN
mapdl.secdata(2.26, 2.26, 8, 0.39, 0.39, 0.22)  # Section data
mapdl.secoffset("USER", "", 0.6465)  # Section offset

BEAM SECTION WITH SECTION ID NUMBER      1 IS OFFSET TO
   OFFSET Y =   0.0000
   OFFSET Z =  0.64650

Define material

Set up the material and its type (a single material), Young’s modulus of 30e6 and Poisson’s ratio of 0.3 is specified.

mapdl.mp("EX", 1, 30e6)
mapdl.mp("PRXY", 1, 0.3)

MATERIAL          1     PRXY =  0.3000000

Define geometry

Set up the nodes and elements. This creates a mesh just like in the problem setup.

mapdl.n(1)  # Node 1
mapdl.n(5, "", 60)  # Node 5 at 60 degrees

# Generate additional nodes
mapdl.fill()

# Define element connectivity
mapdl.e(1, 2)  # Element 1 with nodes 1 and 2

# Generates elements from an existing pattern
mapdl.egen(4, 1, 1)

GENERATE       4 TOTAL SETS OF ELEMENTS WITH NODE INCREMENT OF         1
   SET IS SELECTED ELEMENTS IN RANGE         1 TO         1 IN STEPS OF       1

 MAXIMUM ELEMENT NUMBER=         4

Define coupling and boundary conditions

Fix all degrees of freedom for node 1. Apply a negative force 4000 lb in FY direction at node 5. Apply symmetry boundary condition along z-direction. Then exit prep7 processor.

Effectively, this sets:

\(F = 4000 lb\)

mapdl.d(1, "ALL")  # Fix all degrees of freedom for node 1
mapdl.f(5, "FY", -4000)  # Apply a negative force FY to node 5
mapdl.dsym("SYMM", "Z")  # Apply symmetry boundary condition in Z-direction

# select all entities
mapdl.allsel()
# element plot
mapdl.eplot()

# Finish the pre-processing processor
mapdl.finish()

***** ROUTINE COMPLETED *****  CP =         0.000

Solve

Enter solution mode and solve the system.

mapdl.slashsolu()

# Activate large deflections
mapdl.nlgeom("ON")

# Set convergence tolerances
mapdl.cnvtol("F", "", 1e-4)
mapdl.cnvtol("M", "", 1e-4)

mapdl.solve()  # starts a solution
mapdl.finish()  # exists solution processor

FINISH SOLUTION PROCESSING


 ***** ROUTINE COMPLETED *****  CP =         0.000

Post-processing

Enter post-processing. Compute deflection and stress components.

mapdl.post1()

*****MAPDL VERIFICATION RUN ONLY*****
     DO NOT USE RESULTS FOR PRODUCTION

          ***** MAPDL RESULTS INTERPRETATION (POST1) *****


 USE LAST SUBSTEP ON RESULT FILE  FOR LOAD CASE 0

 SET COMMAND GOT LOAD STEP=     1  SUBSTEP=     1  CUMULATIVE ITERATION=     3
   TIME/FREQUENCY=  1.0000
 TITLE= VM14 LARGE DEFLECTION ECCENTRIC COMPRESSION OF SLENDER COLUMN

Inline functions in PyMAPDL to query node

q = mapdl.queries
end_node = q.node(0, 60, 0)

Retrieve nodal deflection and section stresses

deflection = mapdl.get("DEF", "NODE", end_node, "U", "X")  # Nodal deflection
strss_tens = float(
    mapdl.get("STS_TENS", "SECR", 1, "S", "X", "MAX")[:11]
)  # Maximum section tensile stress
strss_comp = float(
    mapdl.get("STS_COMP", "SECR", 1, "S", "X", "MIN")[:11]
)  # Minimum section compressive stress

# Fill the array with target values
target_def = 0.1086
target_tens = 1803.63
target_comp = -2394.53

data = [
    [target_def, deflection, target_def / deflection],
    [target_tens, strss_tens, target_tens / strss_tens],
    [target_comp, strss_comp, target_comp / strss_comp],
]
col_headers = ["TARGET", "Mechanical APDL", "RATIO"]
row_headers = ["DEFLECTION (in)", "STRSS_TENS (psi)", "STRSS_COMP (psi)"]

Verify the results.

print(pandas.DataFrame(data, row_headers, col_headers))

                     TARGET  Mechanical APDL     RATIO
DEFLECTION (in)      0.1086         0.108815  0.998022
STRSS_TENS (psi)  1803.6300      1807.344850  0.997945
STRSS_COMP (psi) -2394.5300     -2396.000490  0.999386

Finish the post-processing processor.

mapdl.finish()

EXIT THE MAPDL POST1 DATABASE PROCESSOR


 ***** ROUTINE COMPLETED *****  CP =         0.000

Stop MAPDL.

mapdl.exit()